


Next: Elaborando uma teoria geral.
Up: brafman96
Previous: Modelo dinâmico orientado à
Assuma-se a existência, sob controle direto, de c agentes em conformidade
com as leis sociais (i.e. que aplicam a estratégia eficiente) e de p
agentes punitivos, os últimos com a propriedade de observar todas as
instâncias ocorridas do jogo. Existem ainda m agentes maliciosos,
fora de controle direto. As questões relevantes são: O jogo oferece a
possibilidade de punição? Qual é o p.m.m de um jogo? Qual a relação ótima
entre as quantidades de p, c e m? Existe alguma distinção
entre diferentes regras sociais?
Uma estratégia de punição é efetiva se garantir que o máximo payoff esperado
pelo agentes maliciosos não seja maior do que o esperado quando jogando
em acordo com as regras coletivas. Tal garantia é obtida através de uma relação
entre as quantidades de p e c tal que assegure que um agente malicioso
tenha encontros suficientes com agentes punitivos.
Exemplo 1 (continuação): O prejuízo
máximo esperado pelo agente malicioso é 7 (= 2 - (-5)). Isto ocorre quando os
agentes punitivos jogam a estratégia 2. O ganho do agente malicioso contra
o agente ajustado é 8 (= 10 - 2). Assumindo-se que no encontro de dois
maliciosos o ganho esperado é zero e que a distribuição de probabilidades
do encontro entre dois agentes quaisquer é uniforme, é necessário que se tenha
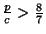 para que os maliciosos tendam ao comportamento
regrado.
para que os maliciosos tendam ao comportamento
regrado.
Como pode ser observado no exemplo, quanto maior a punição, menor o número requerido
de agentes punitivos, o que representa uma vantagem do ponto de vista
da implementação, uma vez que os últimos são mais sofisticados, e.g., devem
identificar desvios de comportamento bem como chavear entre diferentes estratégias
de punição. Para tanto, algumas definições adicionais devem ser feitas.
- Definição 5:
- Um jogo g de 2 jogadores é dito de soma-zero
se para toda estratégia coletiva a soma dos ganhos for 0.
- Definição 6:
- Seja g um jogo de 2 jogadores. Seja
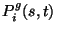 o
ganho do jogador i em g (onde
o
ganho do jogador i em g (onde 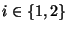 ) quando as estratégias
s e t são jogadas pelos jogadores 1 e 2, respectivamente. O jogo
projetado
) quando as estratégias
s e t são jogadas pelos jogadores 1 e 2, respectivamente. O jogo
projetado 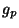 é o seguinte jogo de 2 pessoas de soma-zero: As
estratégias de ambos jogadores são como em g e a matriz de payoffs
é
é o seguinte jogo de 2 pessoas de soma-zero: As
estratégias de ambos jogadores são como em g e a matriz de payoffs
é
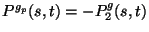 . Define-se o jogo transposto de g,
. Define-se o jogo transposto de g,
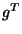 , como sendo o jogo g no qual os papéis dos jogadores se
invertem.
, como sendo o jogo g no qual os papéis dos jogadores se
invertem.
- Definiçao 7:
- Dado um jogo g , uma certa estratégia coletiva
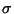 é o equilíbrio de Nash de g se qualquer jogador,
ao aplicar qualquer outra estratégia diversa da que ele aplica em
é o equilíbrio de Nash de g se qualquer jogador,
ao aplicar qualquer outra estratégia diversa da que ele aplica em 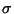 ,
tiver o seu payoff diminuído, sempre que os outros jogadores jogarem
,
tiver o seu payoff diminuído, sempre que os outros jogadores jogarem
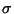 .
.
Reduzir novos conceitos ao equilíbrio de Nash (e.N.)
é conveniente do ponto de vista de projeto, pois esta é uma noção bem compreendida
na teoria dos jogos não cooperativos. Em particular, o e.N. sempre existe
para jogos finitos e os payoffs prescritos em qualquer equilíbrio de
um dado jogo de soma-zero são univocamente definidos.
- Teorema 1:
- Dado um jogo iterativo n-2-g, o p.m.m. é obtido jogando-se
a estratégia do jogador 1 prescrita pelo equilíbrio de Nash do jogo projetado
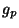 , pela perspectiva do jogador 1; e jogando-se a estratégia do jogador
1 prescrita pelo equilíbrio de Nash do jogo projetado
, pela perspectiva do jogador 1; e jogando-se a estratégia do jogador
1 prescrita pelo equilíbrio de Nash do jogo projetado 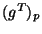 , pela
perpectiva de 2.
, pela
perpectiva de 2.
- Prova:
- Considere-se que o agente punidor assume o papel do jogador 1.
Se o jogador 1 adota a estratégia prescrita pelo e.N.
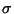 ,
então o jogador 2 não pode obter um ganho maior do que o garantido por
,
então o jogador 2 não pode obter um ganho maior do que o garantido por 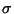 ,
dada simplesmente a definição de e.N. Por seu turno, o jogador 1 não
pode impor maior prejuízo do que jogando a sua estratégia em
,
dada simplesmente a definição de e.N. Por seu turno, o jogador 1 não
pode impor maior prejuízo do que jogando a sua estratégia em 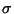 :
para se perceber isto, considere-se que o resultado de 1 não pode ser maior
do que o garantido pelo e.N. (pela própria definição); devido ao fato
ser este um jogo de soma-zero, isto implica que o ganho de 2 não
pode ser menor do que o obtido quando 1 joga em acordo com
:
para se perceber isto, considere-se que o resultado de 1 não pode ser maior
do que o garantido pelo e.N. (pela própria definição); devido ao fato
ser este um jogo de soma-zero, isto implica que o ganho de 2 não
pode ser menor do que o obtido quando 1 joga em acordo com 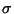 . O
caso do jogador 2 ser o agente punidor é tratado considerando-se o
. O
caso do jogador 2 ser o agente punidor é tratado considerando-se o 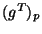 .
.
Exemplo 1 (continuação): O 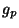 do
dilema do prisioneiro é dado por:
do
dilema do prisioneiro é dado por:
| |
1 (C) |
2 (D) |
| 1 (C) |
-2 |
-10 |
| 2 (D) |
10 |
5 |
sendo o e.N. obtido jogando-se a 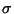 que entrega 5. Neste
caso
que entrega 5. Neste
caso
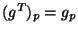 é a estratégia punitiva para ambos jogadores.
é a estratégia punitiva para ambos jogadores.
- Corolário 1:
- Seja n-2-g um jogo iterativo com p agentes punitivos.
Sejam
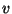 e
e 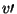 os ganhos do equilíbrio de Nash de
os ganhos do equilíbrio de Nash de 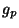 e
e 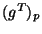 , respectivamente, que neste caso são univocamente definidos.
Sejam
, respectivamente, que neste caso são univocamente definidos.
Sejam 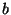 e
e 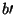 os ganhos máximos que o jogador
1 pode obter em
os ganhos máximos que o jogador
1 pode obter em 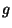 e
e 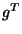 , respectivamente, assumindo-se que o
jogador 2 obedece à convenção social. Sejam
, respectivamente, assumindo-se que o
jogador 2 obedece à convenção social. Sejam 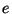 e
e 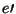 os ganhos dos jogadores 1 e 2, respectivamente, quando ambos jogam a estratégia
coletiva eficiente prescrita pela lei social. Assuma-se que o benefício esperado
de dois agentes maliciosos no seu encontro é nulo. A condição
necessária e suficiente para a existência de uma estratégia de punição é:
os ganhos dos jogadores 1 e 2, respectivamente, quando ambos jogam a estratégia
coletiva eficiente prescrita pela lei social. Assuma-se que o benefício esperado
de dois agentes maliciosos no seu encontro é nulo. A condição
necessária e suficiente para a existência de uma estratégia de punição é:
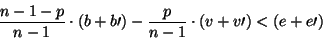 |
(1) |
- Prova:
- O ganho esperado dos agentes maliciosos é
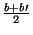 nos encontros com agentes ajustados, e
nos encontros com agentes ajustados, e
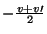 nos
encontros com agentes punitivos Para testar a existência de uma estratégia
punitiva, deve-se considerar o melhor cenário possível da perspectiva do dos
agentes maliciosos, i.e., a não existência de agentes punitivos.
Para se determinar a expectativa de ganho de um agente malicioso deve-se
calcular a média das duas quantidades definidas acima, ponderada pela proporção
entre agentes punitivos e ajustados presentes na população. Procedendo-se
assim, obtem-se:
nos
encontros com agentes punitivos Para testar a existência de uma estratégia
punitiva, deve-se considerar o melhor cenário possível da perspectiva do dos
agentes maliciosos, i.e., a não existência de agentes punitivos.
Para se determinar a expectativa de ganho de um agente malicioso deve-se
calcular a média das duas quantidades definidas acima, ponderada pela proporção
entre agentes punitivos e ajustados presentes na população. Procedendo-se
assim, obtem-se:
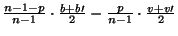 .
Por definição, uma estratégia punitiva existe se, e somente se, a sua expectativa
de utilidade for menor do que a expectativa garantida pela lei social. Uma vez
que a expectativa de utilidade garantida pela obediência à lei social é
.
Por definição, uma estratégia punitiva existe se, e somente se, a sua expectativa
de utilidade for menor do que a expectativa garantida pela lei social. Uma vez
que a expectativa de utilidade garantida pela obediência à lei social é
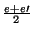 ,
segue que a inequação 1 é verdadeira.
,
segue que a inequação 1 é verdadeira.
O valor da punição,
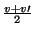 , é indepedente da solução eficiente
e
, é indepedente da solução eficiente
e 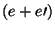 é idêntica para todas soluções eficientes, por definição.
No entanto,
é idêntica para todas soluções eficientes, por definição.
No entanto, 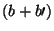 depende da escolha da solução eficiente. Quando
mais de uma solução eficiente existe, a minimização de
depende da escolha da solução eficiente. Quando
mais de uma solução eficiente existe, a minimização de 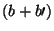 se
torna uma importante consideração no projeto da lei social.
se
torna uma importante consideração no projeto da lei social.
Exemplo 2: Considere-se a seguinte versão do dilema do
prisioneiro:
| |
1 (C) |
2 (D) |
| 1 (C) |
(0,0) |
(-10,10) |
| 2 (D) |
(10, -10) |
(-5,5) |
Neste caso existem 3 soluções eficientes, dadas pelas estratégias coletivas
(1,1), (1,2) e (2,1). No caso de (1,1), 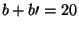 . Já no caso de
(2,1) e (1,2),
. Já no caso de
(2,1) e (1,2), 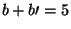 . Claramente, há um incentivo maior para um
desvio da lei social considerando-se a estratégia (1,1) do que (2,1) ou (1,2).
. Claramente, há um incentivo maior para um
desvio da lei social considerando-se a estratégia (1,1) do que (2,1) ou (1,2).



Next: Elaborando uma teoria geral.
Up: brafman96
Previous: Modelo dinâmico orientado à
Carlos Mitidieri
2000-10-28
para que os maliciosos tendam ao comportamento regrado.
do dilema do prisioneiro é dado por:
que entrega 5. Neste caso
é a estratégia punitiva para ambos jogadores.
, é indepedente da solução eficiente e
é idêntica para todas soluções eficientes, por definição. No entanto,
depende da escolha da solução eficiente. Quando mais de uma solução eficiente existe, a minimização de
se torna uma importante consideração no projeto da lei social.
. Já no caso de (2,1) e (1,2),
. Claramente, há um incentivo maior para um desvio da lei social considerando-se a estratégia (1,1) do que (2,1) ou (1,2).