Desempenho em Regime Permanente

O desempenho em regime permanente é medido a partir da capacidade de um sistema seguir referências padrões (salto, rampa, parábola) e a rejeitar assintoticamente sinais de perturbação também padrões.

A ferramenta matemática utilizada na análise do regime permanente é o Teorema do Valor Final, que diz que o valor da saída do sistema quando $t \rightarrow \infty$ (valor da saída em regime permanente) é dada pelo seguinte limite:

$$y(\infty)=\lim_{s \rightarrow 0} s r(s)T(s)$$

onde $r(s)$ é a entrada aplicada ao sistema e $T(s)$ é a função de transferência^1.2 entre $y$ e $r$ .

Consideremos o diagrama da figura (1.10):

Figure 1.10: desempenho em regime permanente

Neste sistema estamos interessados pelos efeitos, em regime permanente, sobre a saída do sistema do sinal $r(s)$ (referência) e da perturbação $q(s)$. Pelo pricípio da superposição temos que:

$$y(s)= \frac{G(s)}{1+G(s)} r(s) + \frac{1}{1+G(s)} q(s)$$

ou seja,

$$y(\infty)= \lim_{s \rightarrow 0} s \frac{G(s)}{1+G(s)} r(s) + \lim_{s \rightarrow 0} s \frac{1}{1+G(s)} q(s)$$

Seguimento de referência

Em sistemas de controle em malha fechada, é desejável que a saída do sistema em regime permanente seja igualada ao sinal de referência (entrada). Entretanto, em alguns casos esta igualdade não é atingida e temos o que chamamos de erro em regime permanente:

$$e(\infty)=r(\infty)-y(\infty)$$

Exemplo:

Considere o diagrama em blocos da figura (1.10) com $q(t)$=0, os gráficos da figura (1.11) mostram a resposta a um salto unitário considerando:

(a)

$G(s)=\displaystyle{\frac{1}{(s+2)}}$

(b)

$G(s)=\displaystyle{\frac{1}{s(s+2)}}$

Figure 1.11: seguimento de referência

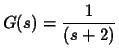
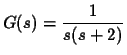
Observe que para (a) o sistema apresenta um erro em regime permanente igual a $0.66$ enquanto que no caso (b) este erro é nulo, ou seja, a saída iguala o valor da referência em regime permanente.

A partir do teorema do valor final, pode-se concluir o seguinte [3]:

• para que um sistema siga, com erro nulo em regime permanente, uma entrada de referência do tipo salto (constante), a função de transferência em malha aberta deve ser no mínimo do tipo 1, ou seja, possuir ao menos 1 pólo na origem. Se o sistema for do tipo 0, teremos um erro finito em regime permanente.

• para que um sistema siga, com erro nulo em regime permanente, uma entrada de referência do tipo rampa (reta), a função de transferência me malha aberta deve ser no mínimo do tipo 2, ou seja, possuir ao menos 2 pólos na origem. Se o sistema for do tipo 1, o sistema apresentará um erro finito e, se for do tipo 0, o erro será infinito, ou seja a referência e a saída do processo irão divergir em regime permanente.

Rejeição a perturbações

Considere que o sistema atingiu o regime permanente com relação a uma determinada entrada de referência. Num dado instante, o sistema é submetido à ação de um sinal externo $q(s)$ que não se extingüe no tempo por si só, por exemplo, um sinal do tipo salto ou rampa. Um sinal deste tipo é chamado perturbação de carga. A identificação exata do ponto de entrada da perturbação em um sistema, em geral, não é fácil determinar, mas pode-se assumir, sem perda de generalidade, que ela é aplicada na saída do processo (como na figura (1.10)) pois é onde seu efeito será sentido.

Exemplo: considere um motor de c.c. que está acionando uma determinada carga a uma velocidade constante. Num dado momento, a carga no eixo do motor é aumentada. Neste caso, a velocidade do motor tende a cair (efeito da perturbação na saída do processo) e duas situações podem ocorrer: ou a velocidade irá estabilizar em um valor menor ou tenderá a se recuperar e voltar ao valor de antes da aplicação da perturbação.

Nos sistemas de controle é desejável que o efeito de perturbações de carga na saída do processo seja minimizado ou completamente anulado, após um determinado período transitório. No primeiro caso dizemos que houve uma rejeição parcial e no segundo uma rejeição assintótica à perturbação.

Exemplo: Considerando as mesmas funções de tranferência do exemplo da página anterior, os gráficos da figura (1.12) mostram a rejeição parcial (caso (a)) e a rejeição assintótica (caso (b)) à uma perturbação do tipo salto.

Figure 1.12: rejeição à perturbações

Intuitivamente, para que um dado sistema em malha fechada rejeite assintoticamente uma dada perturbação, ele deve ser capaz de gerar internamente o sinal da perturbação, com sinal oposto a esta, de maneira a existir um cancelamento. Matematicamente, isto equivale a dizer que o laço de realimentação entre a perturbação e a saída deve possuir os pólos do sinal da perturbação. Seguindo um raciocínio análogo ao feito para o problema de seguimento de referência, é possível então concluir que [3]:

• para um sistema sistema rejeitar assintoticamente uma perturbação do tipo salto, a função de transferência me malha aberta deve ser no mínimo do tipo 1, ou seja, possuir ao menos 1 pólo na origem.

• para um sistema sistema rejeitar assintoticamente uma perturbação do tipo 2, a função de transferência em malha aberta deve ser no mínimo do tipo 2, ou seja, possuir ao menos 2 pólos na origem.

Assim, se o processo a ser controlado não possuir como pólos os pólos da perturbação e desejamos a rejeição assintótica da mesma, deveremos prover o aprecimento destes pólos no laço de realimentação pela introdução de um controlador.