Alocação de Pólos

Considere que o modelo do processo é dado por uma função de transferência estritamente própria de segunda ordem

e o controlador PID tem a função de transferência

$$PID(s) = K_p(1 + T_d s + \frac{1}{T_i s}) = \frac{c_2 s^2+c_1 s + c_0}{s}$$ (4.5)

onde

$$c_2 = K_p T_d$$ (4.6)

$$c_1 = \frac{1}{T_d}$$ (4.7)

$$c_0 = \frac{1}{T_iT_d}$$ (4.8)

Então a função de transferência do sistema em malha fechada é dada por

$$T(s) = \frac{PID(s)G(s)}{1+PID(s)G(s)} = \frac{b_1c_2 s^3 + ... ...(b_1c_1+b_0c_2+a_1) s^2 + (b_1 c_0 + b_0 c_1+a_0) s + b_0 c_0}$$ (4.9)

O método de alocação de pólos consiste em alocar os pólos do sistema em malha fechada em posições pre-especificadas. Os pólos assim escolhidos determinam o polinômio característico de malha fechada $p(s)$. Se os valores escolhidos para os pólos de malha fechada são $p_1$, $p_2$ e $p_3$ então

$$q(s) = (s-p_1)(s-p_2)(s-p_3) = s^3 + q_2 s^2 + q_1 s + q_0$$ (4.10)

Então o ajuste do PID consiste em calcular os parâmetros $c$ que satisfazem à equação abaixo, dita equação diofantina:

$$(b_1c_2+1) s^3 + (b_1c_1+b_0c_2+a_1) s^2 + (b_1 c_0 + b_0 c_1+a_0) s + b_0 c_0 = (b_1c_2+1) . q(s)$$ (4.11)

Equacionando os coeficientes de mesmo grau dos polinômios desta equação e resolvendo para os coeficientes $c$ obtém-se

$$(b_0 b_1) c_2^2 + (b_0 +a_1 b_1 - a_0 b_0 b_1) c_2 + (a_1 -p_2 -a_0b_0b_1 +b_0 b_1 p_1 - b_1^2p_0 ) = 0$$ (4.12)

$$c_1 = \frac{b_0 p_1 - a_0 b_0 (b_1 c_2 + 1) - b_1p_0}{b_1c_2+1}$$ (4.13)

$$c_0 = \frac{p_0}{(b_1c_2+1)b_0}$$ (4.14)

O projeto por alocação de pólos consiste portanto dos seguintes passos:

1. obter um modelo de segunda ordem para o processo;
2. escolher os pólos de malha fechada;
3. calcular os coeficientes $c$ resolvendo a equação (4.13) e em seguida usando as fórmulas (4.14) e (4.15);
4. calcular os parâmetros do controlador a partir de (4.7)-(4.9).

Enquanto os dois últimos passos são triviais e mecânicos, os dois primeiros requerem maior atenção. A obtenção de um modelo na forma (4.5) pode ser relativamente simples através de um ensaio da resposta ao salto do sistema, usando os método dos mínimos quadrados para ajuste dos parâmetros do modelo. Os pólos de malha fechada devem ser escolhidos de forma a garantir o tempo de estabilização exigido. Uma vez que o tempo de estabilização é dado aproximadamente por

$$t_s \approx \frac{4}{\sigma_d}$$ (4.15)

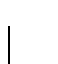onde $-\sigma_d$ é a parte real do pólo dominante, a garantia do tempo de estabilização desejado é alcançada escolhendo todos os pólos com partes reais $\sigma$ tais que

$$\sigma > \frac{4}{t_s}$$ (4.16)

O amortecimento dos pólos de malha fechada^4.2deve ser suficientemente grande a fim de atender requisitos de máxima sobrepassagem e garantir margens de robustez. Finalmente, a fim de minimizar o esforço de controle e portanto a manifestação de efeitos não lineares e dinâmica de alta freqüência, os pólos de malha fechada devem ser tão próximos quanto possível dos pólos de malha aberta, dentro das restrições acima.