Resposta em Freqüência

Considere que a resposta em freqüência do processo é conhecida na forma de um diagrama de Bode. Então o projeto do PID pode ser feito alterando de maneira adequada o formato da resposta em freqüência da função de malha $PID(s)G(s)$ a fim de atender certos critérios. Este procedimento de projeto é conhecido como loop shaping.

Os critério a serem atendidos são valores previamente especificados para a margem de ganho (MG), a margem de fase (MF) e a banda passante (BP). Estes critérios traduzem especificações de rapidez da resposta, sobrepassagem e robustez. Quanto maior a banda passante do função de transferência de malha mais rápida será a resposta do sistema. A margem de fase e a margem de ganho expressam diretamente a robustez do sistema a erros de modelagem. Por outro lado, uma boa margem de fase usualmente garante pequena sobrepassagem. Valores adequados para estes critérios são, para a maioria dos casos:

$$MG > 2$$ (4.17)

$$MF > 45^{o}$$ (4.18)

O projeto consiste então em ajustar a forma do diagrama de Bode da função de transferência de malha de forma a garantir o atendimento destes critérios e obtendo a maior banda passante possível a fim de que a resposta seja a mais rápida possível. Uma ressalva: esta "maximização" da banda passante deve ser feita apenas dentro de certos limites estabelecidos principalmente por considerações relativas à resposta dos atuadores.

Seja o controlador PID dado na forma^4.3

$$PID(s)= K \frac{(s+z1)(s+z_2)}{s(1+s/p)}$$ (4.19)

A resposta em freqüência correspondente é dada na Figura 4.3.

Figure 4.3: Diagrama de Bode para a função de transferência do controlador PID.

A contribuição do pólo da parte derivativa acontece apenas numa faixa de altas freqüências e portanto pode ser desconsiderada durante o projeto. A contribuição dos pólos é dada pela estrutura do controlador, deixando como graus de liberdade apenas as posições dos zeros do controlador e o ganho $K$. Assim, o projeto pode ser iniciado traçando o diagrama de Bode para a parte fixa da função de transferência de malha, ou seja, para a função $F(s)$

$$F(s) = \frac{G(s)}{s}$$ (4.20)

Os zeros devem ser escolhidos de forma a fornecer um avanço de fase na faixa de freqüências de interesse. A seguir o ganho é escolhido de forma a obter as margens especificadas. O método pode ser resumido portano nas seguintes etapas:

1. obter a resposta em freqüência do processo;
2. traçar o diagrama de Bode de $F(s)$ em (4.21);
3. escolher os zeros $z_1$ e $z_2$ fornecendo avanço de fase em torno da freqüência de $180^{o}$;
4. calcular o ganho $K$ que garanta MG e MF adequadas.

A escolha da posição dos zeros exige conhecimento e certa experiência do projetista. Como exemplo, vamos estudar este projeto para processos dados por uma função de transferência do tipo

$$G(s) = \frac{k e^{-Ls}}{Ts+1}$$ (4.21)

e considerar o caso em que o atraso é pequeno, sendo a resposta do sistema dominada pela constante de tempo, ou seja, $L<<T$. O diagrama de Bode da função $G(s)/s$ neste caso é dado na Figura 4.4.

Figure 4.4: Diagrama de Bode para a função de transferência $G(s)/s$ com $L<<T$ (linha cheia) e função compensada (linha tracejada).

Uma vez que o pólo do sistema é lento, os zeros não devem ser alocados próximos a ele pois isto prejudicaria o desempenho na rejeição a perturbações. A fim de obter manter a planura da resposta em freqüência é conveniente manter uma certa distância entre os zeros. Com estas considerações escolhemos os zeros segundo o critério:

$$z_1 = \frac{2}{T}$$ (4.22)

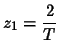$$z_2 = \frac{4}{T}$$ (4.23)

Se o modelo matemático não é conhecido, mas apenas os dados da resposta em freqüência, a constante de tempo pode ser estimada como o inverso da freqüência de corte desta resposta em freqüência. Fazendo o cálculo pelas assíntotas do diagrama de Bode vemos que o ganho de alta freqüência da função compensada é dado por

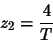$$PID(\jmath w)G(\jmath w)\mid_{w grande} = \frac{K.k.T}{8}$$ (4.24)

Uma vez que esta ganho mantém-se para altas freqüências, este será o ganho na freqüência em que a fase chegar a $180^{o}$ e portanto este ganho deve ser igual ao inverso da margem de ganho desejada. Tem-se assim uma expressão para o cálculo do ganho do controlador:

$$K=\frac{8}{k.T.MG}$$ (4.25)

e com isto o projeto está completo.