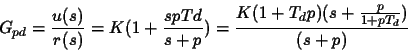O Controlador Proporcional-Derivativo ( PD)

A saída de uma processo apresenta, intuitivamente, uma certa "inércia" com relação a modificações na variável de entrada. Esta "inércia" explica-se pela dinâmica do processo que faz com que uma mudança na variável de controle provoque uma mudaça considerável na saída da planta somente após um certo tempo. Uma outra interpretação é que, dependendo da dinâmica do processo, o sinal de controle estará em "atraso" para corrigir o erro. Este fato é responsável por transitórios com grande amplitude e período de oscilação, podendo, em um caso extremo, gerar respostas instáveis.

A ação derivativa quando combinada com a ação proporcional tem justamente a função de "antecipar" a ação de controle a fim de que o processo reaja mais rápido. Neste caso, o sinal de controle a ser aplicado é proporcional a uma predição da saída do processo.

A estrutura básica do controlador PD é dada por:

$$u(t)= K(e(t) + T_d \frac{de(t)}{dt})$$ (3.3)

Considerando-se que $e(t+T_d)$ pode ser aproximado por

$$e(t+T_d) \approx e(t) + T_d\frac{de(t)}{dt}$$

tem-se que $u(t) \approx K e(t+T_d)$, ou seja, o sinal de controle é proporcional a estimativa do erro de controle $T_d$ unidades de tempo a frente. Em outras palavras, a predição é feita extrapolando o valor do erro pela reta tangente a curva do erro no instant $t$ (vide figura (3.4)).

Figure 3.4: interpretação da ação proporcional-derivativa

Esta ação preditiva tende a aumentar a estabilidade relativa do sistema e a tornar a resposta transitória do mesmo mais rápida.

Na prática, conforme discutido na seção 2.5, deve-se limitar o ganho da parte derivativa em altas-freqüências através do acréscimo de um pólo $p$. A função de transferência do controlado PD é dada então por:

$$G_{pd}=\frac{u(s)}{r(s)}=K (1+ \frac{spTd}{s+p})= \frac{K(1+T_dp)(s+ \frac{p}{1+pT_d})}{(s+p)}$$

Observe que o zero do controlador PD está sempre à direita do pólo. Esta configuração é equivalente à de um compensador de avanço de fase. Note também que ao aumentarmos $T_d$, o zero do controlador tende a origem, significando a predominância da ação derivativa.